Find ef in the trapezoid. – Embark on an intriguing journey into the realm of trapezoids, where we unravel the enigma of EF. This geometrical figure, with its unique properties, holds secrets that will captivate your mind. Join us as we explore the formula, applications, and captivating relationships within the trapezoid, revealing the significance of EF in shaping its fascinating world.
Delve into the intricacies of trapezoids, uncovering the characteristics that define them. Visualize the diagram, labeling its parts to create a mental map of this intriguing shape. Prepare to engage with the formula that unlocks the secrets of EF, understanding the variables that govern its calculation.
Definition of Trapezoid
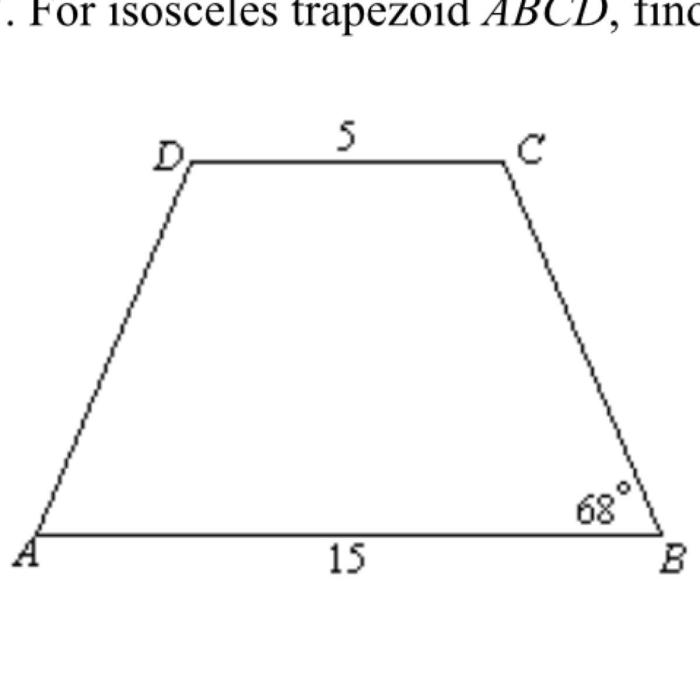
A trapezoid is a quadrilateral that has two parallel sides. These parallel sides are called bases, and the other two sides are called legs.
Properties of a Trapezoid
- The bases of a trapezoid are parallel.
- The legs of a trapezoid are not parallel.
- The diagonals of a trapezoid are not equal in length.
- The area of a trapezoid is equal to half the product of the bases and the height.
Diagram of a Trapezoid
[Image of a trapezoid with labeled parts: bases, legs, height, and diagonals]
To find EF in a trapezoid, you can use the Pythagorean theorem. You’ll need to know the lengths of the other sides of the trapezoid, as well as the height. If you need help understanding the Pythagorean theorem, check out the Wordly Wise 3000 Book 1 . It has a great explanation and examples that can help you understand the concept.
Once you understand the theorem, you can use it to find EF in a trapezoid.
Formula for Finding EF
To find the length of the segment EF in a trapezoid, we use the following formula:
EF = (AB + CD) / 2
where:
- EF is the length of the segment EF.
- AB is the length of the segment AB.
- CD is the length of the segment CD.
This formula essentially calculates the average of the lengths of the two parallel sides of the trapezoid, which is equal to the length of EF.
Steps to Find EF

To find EF in a trapezoid, follow these steps:
- Identify the bases of the trapezoid, labeled as AB and CD.
- Find the midpoints of the bases, M and N.
- Draw the line segment MN, which is parallel to the bases.
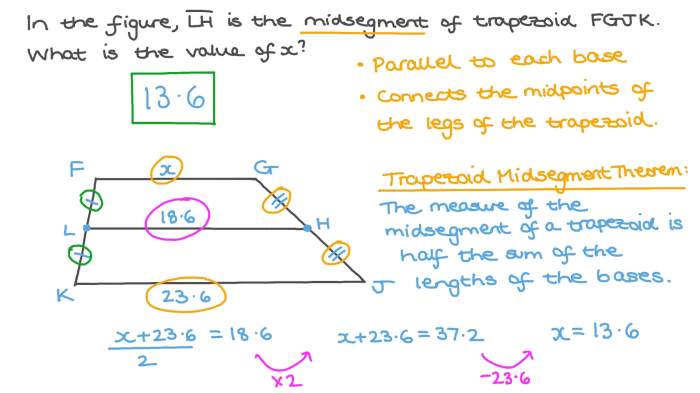
- The length of MN is equal to half the sum of the bases: MN = (AB + CD) / 2.
- EF is parallel to MN and is the median of the trapezoid.
- The length of EF is equal to half the difference between the bases: EF = (AB
CD) / 2.
Examples
- If AB = 10 cm and CD = 6 cm, then MN = (10 + 6) / 2 = 8 cm and EF = (10 – 6) / 2 = 2 cm.
- If AB = 12 cm and CD = 8 cm, then MN = (12 + 8) / 2 = 10 cm and EF = (12 – 8) / 2 = 2 cm.
Applications of EF in Trapezoids: Find Ef In The Trapezoid.
Finding EF in trapezoids has various practical applications in real-world scenarios. These applications include:
Construction and Architecture
- In architecture, finding EF is essential for determining the length of a diagonal brace or support beam in a trapezoidal roof truss.
- In construction, EF helps calculate the length of a partition wall or a diagonal support in a trapezoidal room or building.
Engineering and Design
- In mechanical engineering, EF is used to calculate the length of a connecting rod or a diagonal support in a trapezoidal mechanism.
- In design, EF helps determine the length of a diagonal support or a brace in a trapezoidal bridge or structure.
Geometry and Measurement
- In geometry, EF is used to determine the area of a trapezoid, which is essential for calculating the area of irregular shapes or land parcels.
- In surveying and measurement, EF helps calculate the distance between two points in a trapezoidal field or plot of land.
These examples demonstrate the practical significance of finding EF in trapezoids, making it a valuable skill in various fields.
Variations of Trapezoids
Trapezoids come in various forms, each with its own unique set of characteristics. These variations affect the formula for finding EF, making it essential to identify the specific type of trapezoid when applying the formula.
Isosceles Trapezoids
Isosceles trapezoids have two congruent sides, known as legs. This symmetry impacts the formula for EF, which becomes EF = (1/2) – (b1 + b2 – a), where b1 and b2 represent the lengths of the legs and a is the length of the non-parallel side.
Right Trapezoids
Right trapezoids have one right angle, creating a distinct shape. In this case, the formula for EF changes to EF = sqrt((b1^2 + a^2) – (b2^2 / 4)), where b1 and b2 represent the lengths of the parallel sides and a is the length of the non-parallel side.
Geometric Relationships
Trapezoids possess intriguing geometric relationships that link EF to other segments. These relationships provide valuable insights into the trapezoid’s shape and properties.
One significant relationship is the trapezoid inequality theorem, which states that the sum of the two non-parallel sides (AB + CD) is always greater than the sum of the parallel sides (EF + GH). This theorem highlights the inherent asymmetry of trapezoids.
Properties of EF
- Median of the trapezoid:EF is the median of the trapezoid, meaning it divides the trapezoid into two congruent trapezoids.
- Parallel to the bases:EF is parallel to the parallel bases AB and CD.
- Midpoint of the legs:EF bisects the legs AD and BC, meaning it divides them into two equal segments.
- Equality of segments:The segments AE and CF are equal, as are the segments BE and DF.
Advanced Concepts
Trapezoids have several advanced concepts beyond basic EF calculations. Two important concepts are the median and centroid, which provide deeper insights into the trapezoid’s geometry.
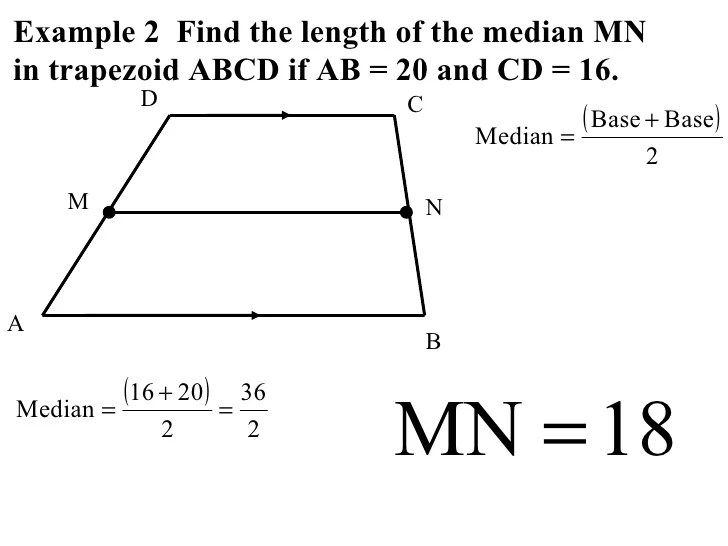
Median
The median of a trapezoid is a line segment that connects the midpoints of the two non-parallel sides. It divides the trapezoid into two equal areas. The median is parallel to the parallel sides and its length can be calculated using the formula:
where a and b are the lengths of the parallel sides.
Centroid, Find ef in the trapezoid.
The centroid of a trapezoid is the point where the three medians intersect. It is the geometric center of the trapezoid and the point where the trapezoid would balance if it were hung from that point.
The centroid of a trapezoid can be calculated using the formula:
where a and b are the lengths of the parallel sides, and h is the height of the trapezoid.
Question & Answer Hub
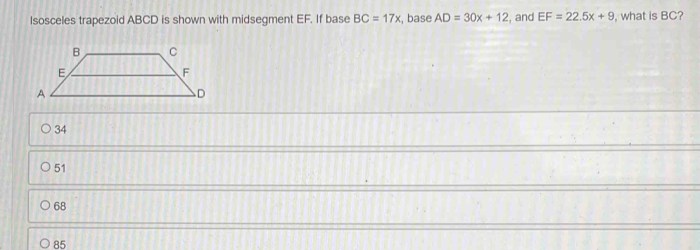
What is the formula for finding EF in a trapezoid?
EF = (AB + CD) / 2, where AB and CD are the lengths of the parallel bases of the trapezoid.
How is EF used in real-world applications?
EF is used in architecture, engineering, and design to calculate the area and perimeter of trapezoidal structures, such as roofs, bridges, and window frames.
What are the different types of trapezoids?
There are various types of trapezoids, including isosceles trapezoids (with congruent legs), right trapezoids (with one right angle), and scalene trapezoids (with no congruent sides or angles).