Probability and two-way tables assignment – Embark on an illuminating journey into the realm of probability and two-way tables, where we unravel the intricacies of data analysis. Discover the fundamental concepts, practical applications, and the power they hold in deciphering the world around us.
From everyday occurrences to complex scientific inquiries, probability and two-way tables provide a robust framework for understanding the likelihood of events and making informed decisions based on data.
Probability Basics
Probability is a fundamental concept in data analysis that quantifies the likelihood of an event occurring. It plays a crucial role in understanding and predicting the behavior of data, enabling us to make informed decisions based on the probability of various outcomes.
In everyday life, we encounter probability in countless situations. For instance, when we flip a coin, we know that the probability of landing on heads is 1/2. Similarly, when we draw a card from a standard deck, the probability of drawing an ace is 4/52.
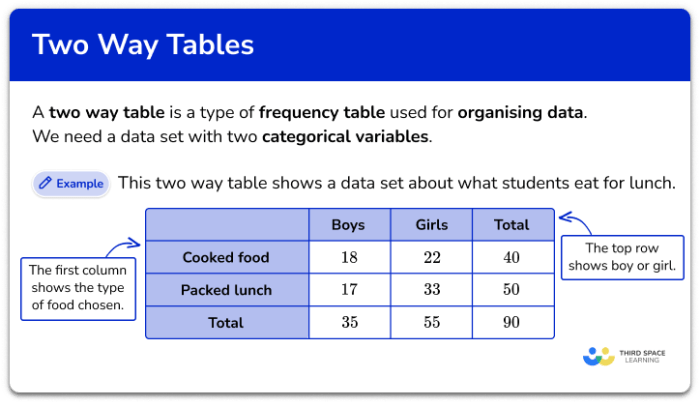
Two-Way Tables

Two-way tables, also known as contingency tables, are a powerful tool for organizing and summarizing data that involves two categorical variables. They allow us to visualize the relationship between these variables and calculate probabilities based on the observed frequencies.
To create a two-way table, we arrange the categories of one variable in rows and the categories of the other variable in columns. The cells of the table contain the counts or frequencies of observations that fall into each combination of categories.
Joint Probability, Probability and two-way tables assignment
Joint probability refers to the probability of two events occurring together. In the context of two-way tables, joint probability is represented by the count or frequency of observations that fall into a specific cell.
For example, in a two-way table that shows the relationship between gender and occupation, the joint probability of being female and working as a doctor would be the count of female doctors in the corresponding cell.
Marginal Probability
Marginal probability refers to the probability of an event occurring regardless of the other variable. In two-way tables, marginal probabilities are calculated by summing the counts or frequencies in each row or column.
For instance, in the gender and occupation example, the marginal probability of being female would be the sum of the counts of female doctors, female teachers, and female lawyers in the corresponding row.
Conditional Probability
Conditional probability refers to the probability of an event occurring given that another event has already occurred. In two-way tables, conditional probability is calculated by dividing the joint probability of the two events by the marginal probability of the condition.
For example, the conditional probability of being a doctor given that you are female would be the joint probability of being female and a doctor divided by the marginal probability of being female.
Independence
Independence in probability refers to the lack of relationship between two events. In the context of two-way tables, two events are considered independent if the joint probability of the events is equal to the product of their marginal probabilities.
For instance, in the gender and occupation example, if the events of being female and being a doctor are independent, then the joint probability of being female and a doctor would be equal to the product of the marginal probability of being female and the marginal probability of being a doctor.
Applications of Two-Way Tables and Probability
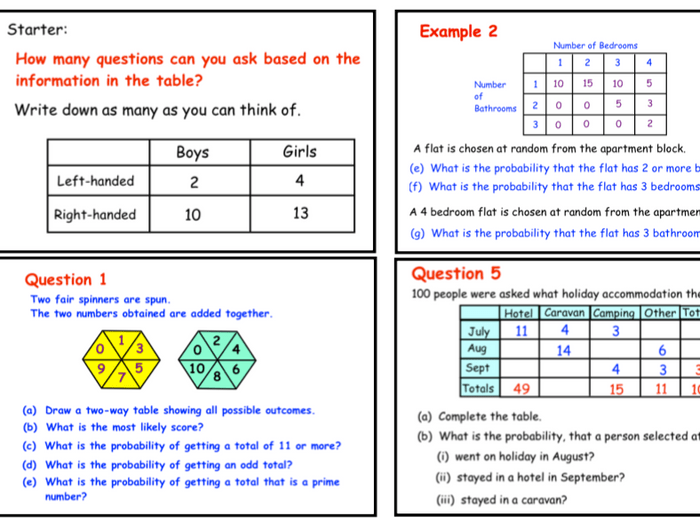
Two-way tables and probability have wide-ranging applications in various fields, including:
- Market research: Understanding consumer preferences and market trends
- Epidemiology: Identifying risk factors and disease prevalence
- Social sciences: Analyzing social patterns and relationships
- Quality control: Assessing product quality and identifying defects
- Business intelligence: Making informed decisions based on data
Essential FAQs: Probability And Two-way Tables Assignment
What is the significance of probability in data analysis?
Probability plays a pivotal role in data analysis by quantifying the likelihood of events, enabling us to make informed predictions and draw meaningful conclusions from data.
How do two-way tables enhance our understanding of data?
Two-way tables provide a visual representation of the relationship between two categorical variables, allowing us to identify patterns, trends, and associations that may not be apparent from raw data.
What is the difference between joint and marginal probability?
Joint probability measures the likelihood of two or more events occurring simultaneously, while marginal probability focuses on the probability of a single event occurring, regardless of other events.
How can conditional probability help us make better decisions?
Conditional probability enables us to determine the likelihood of an event occurring given that another event has already occurred, providing valuable insights for decision-making in uncertain situations.
What is the concept of independence in probability?
Independence in probability refers to the scenario where the occurrence of one event does not affect the probability of another event occurring, simplifying the analysis and interpretation of data.